티스토리 뷰
- 앞의 t-test에서, 이상치와 왜도를 통해 그 결과가 건강한지 살펴보았습니다.
- ANOVA 는 이러한 제약이 조금 더 타이트하며, 다른 통계학 모형들 또한 그런 경우가 많습니다.
- ANOVA와 많은 모형들은 원본 Raw 데이터가 아닌 잔차Residual 에 대한 가정을 가집니다.
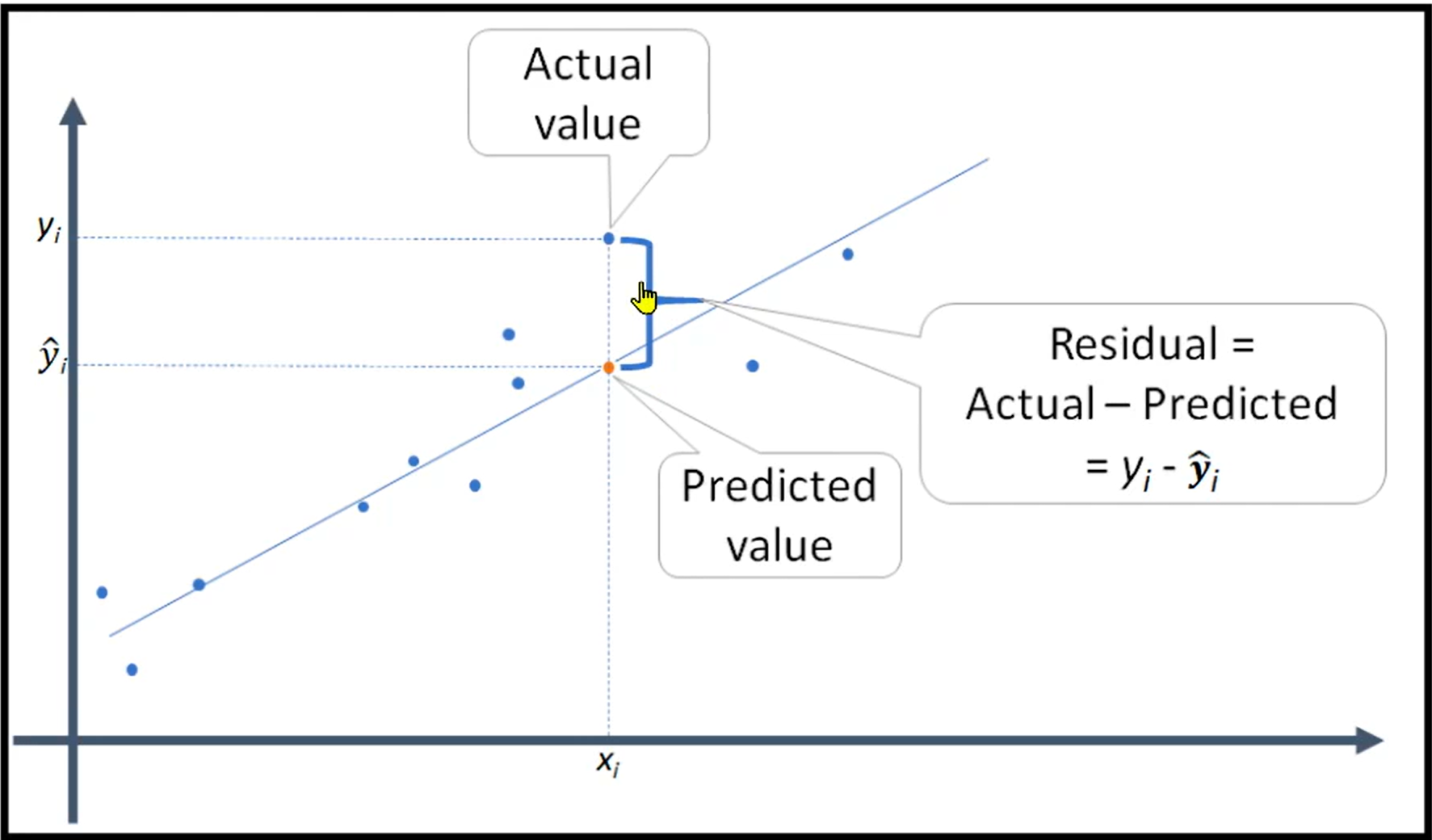
정규성 Normality
- 잔차의 분포가 정규분포를 따름을 가정합니다.
- 가장 흔한 문제는 앞에서 보았던 왜도Skewnes와 이상치Outlier이며, 가장 중대한 문제입니다.
- QQplot 을 통해 시각적으로 확인할 수 있습니다.

- 통계적 검사를 통해 이를 진단할 수도 있습니다.
-Shapiro 는 소표본 (N<=50) 일 때 유용합니다.
Kolmogorov 는 비교적 대표본일 때 유용합니다.
- 데이터가 지나치게 많을 때 (>1,000,000) 는 샘플링하여 검사한느 것도 좋습니다. - 로그 변환 Log transformation 와 이상치 제거로 해결되는 경우가 대다수 입니다.
등분산성Homoscadasticity
- 각 집단의 분산은 동일하다는 가정입니다.
- 이름이 어려워보이는데, 등분산성 Equal variance 이라고 쉽게 말하기도 합니다.
- 이분산성은 조금 어렵게 말하면 Hetero-scadasticity 라고 합니다.

- t-test 에서는 두 집단의 분산이 다르더라도 이를 보정할 수 있었지만, ANOVA는 그게 조금 더 어렵습니다.
가정이 어긋날시 2종 오류의 위험이 커집니다.일반적으로 바틀렛Bartlett 검정을 많이 사용 합니다. - 정규성을 교정하면 해결되는 경우가 많습니다.

독립성 Independency
- 각 관측치가 독립적으로 분포하였다는 의미로, 앞에서 봤던 iid에서의 independence 입니다.
- 풀어말하면, 각 데이터의 순서에 따른 패턴이 존재하지 않아야 한다는 것이며 패턴이 존재하는 것을
자기 상관성 Auto-correlation 이라고도 합니다. - 편향 bias 에는 문제가 생기지 않고, 비교적 가장 약한 위험입니다. 일반적으로 DW 검정을 통해 진단합니다.
- 데이터가 시간에 따라 분포하는 경우 생기기 쉽습니다.
- 예시 1 : 일자별 데이터
- 예시 2 : 가입 순서에 따라 정렬된 유저 데이터 - 잔차에 대한 시계열 Time-series 모형을 적합Fit 할 수 있지만, 여기서는 생략 합니다.
FAQ
ANOVA vs t-test
- 집단이 2개일 때 ANOVA 를 할 수 있을까요? 그러면 어떻게 될까요?
- 할 수 있고, t-test와 정확히 같은 결과를 보여줍니다. 정확히는 양측 two-tailed 검정일 때 그렇습니다.
- 이것이 가능한 이유는 t2 =F 와 같은 분포 사이의 관계 덕분입니다. - 신뢰 수준을 쭉 높이고 t-test를 여러 번 하면 안되나요 ?
- 가능합니다. 이를 본페로니Bonferroni 방법이라고 합니다.
사실 데이터가 충분하면 본페로니를 쓰지 말아야 할 이유는 없지만, 집단의 수에 따라 신뢰 구간을 생각보다 많이 조절해야 합니다.
더보기
- 수학, 얼마나 해야 하나요 ?
수학 공부를 따로 햇거라도 통계학과 머신러닝을 깊이 있게 공부하고 싶은 분들을 위한 가이드 입니다.
문과 수준의 중고등 수학은 알고 있다고 가정합니다. 거기서 헤매시는데 중고등 수학이 싫으신 분은
칸 아카데미를 추천드립니다. - 대학 과정의 수학으로는 2가지가 필수 입니다.
미적분 : 대학 교재 수준으로 한 권 정도
선형대 : 대학 교재 수준으로 한 권 정도 (길버트 스트랭이 명저이며, 유투브 강의가 필수입니다.) - 그 외에 좋은 것으로는
해석학 : 수학이 어떻게 돌아가는지를 알 수 있습니다. 한국어로 이슬비님이 유명하십니다.
수치해석학 : 수치를 다루고 최적화 할 때 유용하다고 합니다.
행렬미적 : 위의 과목에서 행렬과 벡터를 미적하는 걸 안 배웠다면 따로 공부해두시는 게 좋습니다.
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
최근에 올라온 글
최근에 달린 댓글
글 보관함
링크
TAG
- 머신러닝
- 데이터 시각화
- 데이터 분석 주니어
- BA
- 프로덕트 분석가
- 설레다
- 데이터 분석가
- 기획자
- 프로덕트 매니저
- A/B테스트
- 아하 모먼트
- 퍼포먼스 마케팅
- BI
- 북극성 지표
- 아무일 없는것처럼
- ADsP
- 데이터 리터러시
- 프로젝트 매니저
- 데이터분석가
- 퍼포먼스 마케터
- 방법론
- 통계학
- 데이터 분석가 주니어
- 알고리즘
- 빅데이터
- 데이터 분석
- 그로스 해킹
- 책 추천
- 빅테크
- PM
- Total
- Today
- Yesterday
